Problem: Operations with Numbers
Write a program that reads two integers (n1 and n2) and an operator that performs a particular mathematical operation with them. Possible operations are: summing up (+), subtraction (-), multiplying (*), division (/) and modular division (%). Upon summing up, subtracting and multiplying, the console must print the result and display whether it is even or odd number. Upon regular division – just the result, and upon modular division – the remainder. You need to take into consideration the fact that the divisor can be equal to zero (= 0) and dividing by zero is not possible. In this case, a special notification must be printed.
Input Data
3 lines are read from the console:
- N1 – integer within the range [0 … 40 000].
- N2 – integer within the range [0 … 40 000].
- Operator – one character among: "+", "-", "*", "/", "%".
Output Data
Print the output as a single line on the console:
- If the operation is summing up, subtraction or multiplying:
- "{N1} {operator} {N2} = {output} – {even/odd}".
- If the operation is division:
- "{N1} / {N2} = {output}" – the result is formatted up to the second digit after the decimal point.
- If the operation is modular division:
- "{N1} % {N2} = {remainder}".
- In case of dividing by 0 (zero):
- "Cannot divide {N1} by zero".
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 123 12 / |
123 / 12 = 10.25 | 112 0 / |
Cannot divide 112 by zero |
| 10 3 % |
10 % 3 = 1 | 10 0 % |
Cannot divide 10 by zero |
| Input | Output |
|---|---|
| 10 12 + |
10 + 12 = 22 - even |
| 10 1 - |
10 - 1 = 9 - odd |
| 7 3 * |
7 * 3 = 21 - odd |
Hints and Guidelines
The problem is not complex, but there are a lot of code lines to write.
Processing the Input Data
Upon reading the requirements, we understand that we expect three lines of input data. The first two lines enter two integers (within the specified range), and the third line – an arithmetical symbol.

Condition for 0
Let's create and initialize the variables needed for the logic and calculations. In one variable we will store the calculations output, and the other one we will use for the final output of the program.
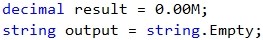
When carefully reading the requirements, we understand that there are cases where we don't need to do any calculations, and simply display a result.
Therefore, we can first check if the second number is 0 (zero), as well as whether the operation is division or modular division, and then initialize the output.

Let's place the output as a value upon initializing the output parameter. This way we can apply only one condition – whether it is needed to recalculate or replace this output.
Based on the approach that we choose, our next condition will be either a simple else or a single if. In the body of this condition, using additional conditions regarding the manner of calculating the output based on the passed operator, we can separate the logic based on the structure of the expected output.
Condition for Division and Modular Division
From the requirements we can see that for summing up (+), subtraction (-) or multiplying (*) the expected output has the same structure: "{n1} {operator} {n2} = {output} – {even/odd}", whereas for division (/) and modular division (%) the output has a different structure.

Condition for Summing Up, Subtraction and Multiplying
We finish the solution by applying conditions for summing up, subtraction and multiplying:

For short and clear conditions, such as the above example for even and odd number, you can use a ternary operator. Let's examine the possibility to apply a condition with or without a ternary operator.
Using Ternary Operator
Without using a ternary operator the code is longer but easier to read:

Upon using a ternary operator the code is much shorter but may require additional efforts to read and understand the logic:
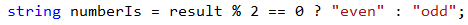
Printing the Output
Finally, what remains is to print the calculated result on the console:

Testing in the Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/509#2.