Problem: Crossing Sequences
We have two sequences:
- a sequence of Tribonacci (by analogy with the Fibonacci sequence), where each number is the sum of the previous three (with given three numbers)
- a sequence generated by a numerical spiral defined by looping like a spiral (right, bottom, left, top, right, bottom, left, top, etc.) of a matrix of numbers starting from its center with a given starting number and incremental step, by storing the current numbers in the sequence each time we make a turn
Write a program that finds the first number that appears in both sequences defined in the aforementioned way.
Example
Let the Tribonacci sequence start with 1, 2 and 3. This means that the first sequence will contain the numbers 1, 2, 3, 6, 11, 20, 37, 68, 125, 230, 423, 778, 1431, 2632, 4841, 8904, 16377, 30122, 55403, 101902, and so on.
At the same time, let the numbers in the spiral begin with 5 and the spiral increases by 2 at each step.
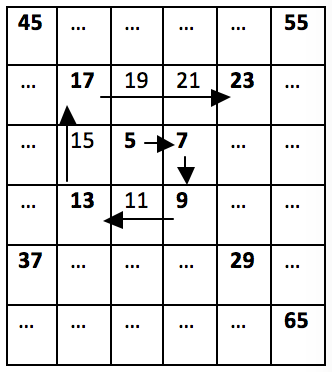
Then the second sequence will contain the numbers 5, 7, 9, 13, 17, 23, 29, 37 and so on. We see that 37 is the first number to be found in the Tribonacci sequence and in the spiral one, and that is the desired solution to the problem.
Input Data
Input data should be read from the console.
- On the first three lines of the input we will read three integers, representing the first three numbers in the Tribonacci sequence, positive non-zero numbers, sorted in ascending order.
- On the next two lines of the input we will read two integers representing the first number and the step for each cell of the matrix for the spiral of numbers. The numbers representing the spiral are positive non-zero numbers.
Input data will always be valid and will always be in the format described. No need to check.
Output Data
The result should be printed on the console.
On the single line of the output, we must print the smallest number that occurs in both sequences. If there is no number in the range [1 … 1 000 000], which can be found in both sequences, print "No".
Constraints
- All numbers in the input will be in the range [1 … 1 000 000].
- Allowed program time: 0.3 seconds.
- Allowed memory: 16 MB.
Sample Input and Output
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 1 2 3 5 2 |
37 | 13 25 99 5 2 |
13 | 99 99 99 2 2 |
No |
| Input | Output | Input | Output |
|---|---|---|---|
| 1 1 1 1 1 |
1 | 1 4 7 23 3 |
23 |
Hints and Guidelines
The problem seems quite complicated, so we will break it into simpler sub-problems.
Processing the Input
The first step in solving the problem is to read and process the input. Input data consists of 5 integers: 3 for the Tribonacci sequence and 2 for the numerical spiral.

Once we have the input data, we need to think about how we will generate the numbers in the two sequences.
Generating Tribonacci Sequence
For the Tribonacci sequence we will always collect the previous three values and then move the values of those numbers (the three previous ones) one position in the sequence, i.e. the value of the first one must accept the value of the second one, and so on. When we are done with the number, we will store its value in an array. Since the problem description states that the numbers in the sequences do not exceed 1,000,000, we can stop generating this range at exactly 1,000,000.

Generating Numerical Spiral
We need to think of a relation between numbers in the numerical spiral so we can easily generate every next number without having to look at matrices and loop through them. If we carefully look at the picture from the description, we will notice that every 2 "turns" in the spiral, the numbers we skip are increased by 1, i.e. from 5 to 7 and from 7 to 9, not a single number is skipped, but we directly add with the step of the sequence. From 9 to 13 and from 13 to 17 we skip a number, i.e. we add the step twice. From 17 to 23 and from 23 to 29 we skip two numbers, i.e. we add the step three times and so on.
Thus, we see that for the first two we have the last number + 1 * the step, the next two we add with the 2 * the step and so on. Every time we want to get to the next number of the spiral, we will have to make such calculations.
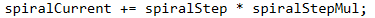
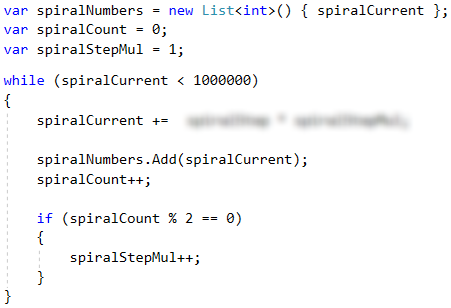
What we have to take care of is for each two numbers, our multiplier (let's call it "coefficient") must increase by 1 (spiralStepMul++), which can be achieved with a simple check (spiralCount % 2 == 0). The whole code from the generation of the spiral in an array is given below.
Finding Common Number for the Sequences
Once we have generated the numbers in both sequences, we can proceed to unite them and build the final solution. How will it look? For each of the numbers in the first sequence (starting from the smaller one) we will check if it exists in the other one. The first number that meets this criterion will be the answer to the problem.
We will do a linear search in the second array, and we will leave the more curious participants to optimize it using the technique called binary search because the second array is generated in sorted form, i.e. it meets the requirement to apply this type of search. The code for finding our solution will look like this:

Alternative Solution
The previous solution to the problem uses arrays to store the values. Arrays are not needed to solve the problem. There is an alternative solution that generates the numbers and works directly with them instead of keeping them in an array. On every step we can check whether the numbers in the two sequences match. If this is the case, we will print the number on the console and terminate the execution of our program. Otherwise, we will see the current number of which sequence is the smaller one and we will generate the next one where we are "lagging". The idea is that we will generate numbers from the sequence that is "behind" until we skip the current number of the other sequence and then vice versa, and if we find a match in the meantime, we will terminate the execution.

Testing in the Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/518#0.