Problem: Diamond
Write a program that takes an integer n (1 ≤ n ≤ 100) and prints a diamond with size n, as in the following examples:
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 1 | * |
2 | ** |
3 | -*-*-*-*- |
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 4 | -**-*--*-**- |
5 | --*---*-*-*---*-*-*---*-- |
6 | --**---*--*-*----*-*--*---**-- |
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 7 | ---*-----*-*---*---*-*-----*-*---*---*-*-----*--- |
8 | ---**-----*--*---*----*-*------*-*----*---*--*-----**--- |
9 | ----*-------*-*-----*---*---*-----*-*-------*-*-----*---*---*-----*-*-------*---- |
Video: Draw a Diamond
Watch this video lesson to learn how to print a diamond on the console using nested loops: https://youtu.be/Z8crtxDztBk.
Hints and Guidelines
What we know from the problem explanation is that the diamond is with size n x n.
From the example input and output we can conclude that all rows contain exactly n symbols, and all the rows, with the exception of the top and bottom ones, have 2 stars. We can mentally divide the diamond into 2 parts:
- Upper part. It starts from the upper tip down to the middle.
- Lower part. It starts from the row below the middle one and goes down to the lower tip (inclusive).
Upper Part
- If n is an odd number, it starts with 1 star.
- If n is an even number, it starts with 2 stars.
- With each row down, the stars get further away from each other.
- The space between, before and after the stars is filled up with dashes.
Lower Part
- With each row down, the stars get closer to each other. This means that the space (the dashes) between them is getting smaller and the space (the dashes) on the left and on the right is getting larger.
- The bottom-most part has 1 or 2 stars, depending on whether n is an even or odd number.
Upper and Lower Parts of the Diamond
- On each row, except the middle one, the stars are surrounded by inner and outer dashes.
- On each row there is space between the two stars, except on the first and the last row (sometimes the star is 1).
Reading the Input Data
We read n from the console and we save it in a variable of int type.
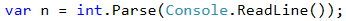
Printing the Top Part of the Diamond
We start drawing the upper part of the diamond. The first thing we need to do is to calculate the number of the outer dashes leftRight (the dashes on the outer side of the stars). It is equal to (n - 1) / 2, rounded down.
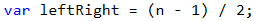
After we have calculated leftRight, we start drawing the upper part of the diamond. We can start by running a loop from 0 to n / 2 + 1 (rounded down).
At each iteration of the loop the following steps must be taken:
- We draw on the console the left dashes (with length
leftRight) and right after them the first star.

- We will calculate the distance between the two stars. We can do this by subtracting from n the number of the outer dashes, and the number 2 (the number of the stars, i.e. the diamonds outline). We need to store the result of the subtraction in a variable
mid.

- If
midis lower than 0, we know that on the row there should be only 1 star. If it is higher or equal to 0 then we have to print dashes with lengthmidand one star after them. - We draw on the console the right outer dashes with length
leftRight.

- In the end of the loop we decrease
leftRightby 1 (the stars are moving away from each other).
We are ready with the upper part.
Printing the Bottom Part of the Diamond
Printing the lower part is very similar to that of the upper part. The difference is that instead of decreasing leftRight with 1 in the end of the loop, we will increase leftRight with 1 at the beginning of the loop. Also, the loop will be from 0 to (n - 1) / 2.
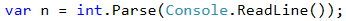
| Repeating a code is considered bad practice, because the code becomes very hard to maintain. Let's imagine that we have a piece of code (e.g. the logic for drawing a row from the diamond) at a few more places and we decide to change it. For this we will have to go through all the places and change it everywhere. Now let's imagine that you need to reuse a piece of code not 1, 2 or 3 times but tens of times. A way to overcome this problem is to use methods. You can look for additional information for methods in the Internet or to look at Chapter “10” (Methods). |
If we have written all correctly, then the problem is solved.
Testing in the Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/512#9.