Problem: Sequence of Increasing Elements

The next sample exam problem is about finding the longest increasing subsequence of given sequence of integers.

Video: Sequence of Increasing Elements

Watch the video lesson about solving the "Sequence of Increasing Elements" problem: https://youtu.be/4ZHRC4usRAM.

Problem Description

A series of n numbers is given: a1, a2, …, an. Calculate the length of the longest increasing sequence of consecutive elements in the series of numbers.

Input

The input data is read from the console. The first line holds an integer n (0 ≤ n ≤ 1000). On the following n lines we are given n integers in the range [-1000 … 1000]: a1, a2, …, an.

Output

On the console we must print one number – the length of the longest increasing sequence.

Sample Input and Output

Reading the Input Data and Creating Additional Variables

To solve this problem, we need to think in a bit more algorithmic way. A sequence of numbers is given to us, and we need to check whether each subsequent one will be larger than the previous one, and if so, we count how long is the sequence in which this condition is fulfilled. Then we have to find which sequence of these is the longest one. To do this, let's create some variables that we will use during solving the problem.

The variable n is the count of numbers we get from the console. In countCurrentLongest we will keep the number of elements in the increasing sequence we are currently counting. For example, in the sequence: 5, 6, 1, 2, 3 countCurrentLongest will be 2 when we reach the second element of the counting (5, 6, 1, 2, 3) and will become 3 when we reach the last element (5, 6, 1, 2, 3), because the increasing row 1, 2, 3 has 3 elements. We will use countLongest to keep the longest increasing sequence. The other variables are a – the number we are currently in, and aPrev – the previous number which we will compare with a to see if the row is growing.

Determining Increasing Sequence

We begin to run the numbers and check if the present number a is larger than the previous aPrev one. If this is true, then the row is growing, and we need to increase its number by 1. This is stored in the variable that tracks the length of the sequence we are currently in – countCurrentLongest. If the number a is not greater than the previous one, it means that a new sequence starts, and we have to start the count from 1. Finally, after all the checks are done, aPrev becomes the number we are currently using, and we start the loop from the beginning with the next entered a.

Here is a sample implementation of the algorithm described:

Finding and Printing the Longest Sequence

What remains is to see which of all sequences is the longest one. We will do this by checking in the loop if the sequence we are currently in has become longer than the longest one by now. The whole loop will look like this:

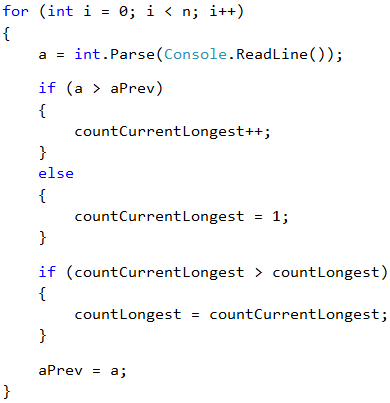
Finally, we print the length of the longest sequence found.

Testing in the Judge System

Test your solution here: https://judge.softuni.org/Contests/Practice/Index/516#7.