Problem: Distance
Write a program that calculates what is the distance passed by a car (in kilometers), if we know the initial speed (km/h), the initial time frame in minutes, then the speed is increased by 10%, the second time frame, then the speed is decreased by 5%, and the time until the end of the trip. In order to calculate the distance, you need to convert the minutes into hours (for example 70 minutes = 1.1666 hours).
Input Data
The input comes from the console and consists of 4 lines:
- The initial speed in km/h – an integer within the range [1 … 300].
- The first time frame in minutes – an integer within the range [1 … 1000].
- The second time frame in minutes – an integer within the range [1 … 1000].
- The third time frame in minutes – an integer within the range [1 … 1000].
Output Data
Print a number on the console: the kilometers passed, formatted up to the second digit after the decimal point.
Sample Input and Output
| Input | Output | Comments |
|---|---|---|
| 90 60 70 80 |
330.90 | Distance with initial speed: 90 km/h * 1 hour (60 min) = 90 km After speed increase: 90 + 10% = 99.00 km/h * 1.166 hours (70 min) = 115.50 km After speed decrease: 99 - 5% = 94.05 km/h * 1.33 hours (80 min) = 125.40 km Total number of km passed: 330.9 km |
| Input | Output | Comments |
|---|---|---|
| 140 112 75 190 |
917.12 | Distance with initial speed: 140 km/h * 1.86 hours (112 min) = 261.33 km After speed increase: 140 + 10% = 154.00 km/h * 1.25 hours (75 min) = 192.5 km After speed decrease: 154.00 - 5% = 146.29 km/h * 3.16 hours (190 min) = 463.28 km Total number of km passed: 917.1166 km |
Hints and Guidelines
It is possible that such a description may look misleading and incomplete at first glance, which adds to the complexity of a relatively easy task. Let's separate the problem into a few sub-problems and try to solve each of them one by one, which will lead us to the final result:
- Our initial sub-problem will be to read the input data entered by the user, and store them in appropriate variables.
- Execution of the main programming logic, which in our case is a batch of simple calculations of the properties that we already have.
- Calculation and shaping up the end result.
The main part of the programming logic is to calculate what will be the distance passed after all changes in speed. As during execution of the program, part of the data that we have is modified, we could separate the program code into a few logically separated parts:
- Calculation of the distance passed with initial speed.
- Change of speed and calculation of the distance passed.
- Last change of speed and calculation.
- Summing up.
Reading the Input Data
We use the following function to read the data from the console:

By definition, the input data is given as four separate lines. This is why we need to execute the previous code four times in total.

Selecting Data Type for Calculations
In order to perform the calculations, we select decimal type.
The data type for real numbers with decimal representation in C# is the 128-bit decimal type. It has the accuracy of 28 to 29 decimal numbers. Its minimum value is -7.9×10^28, and its maximum value is +7.9×10^28. Its default value is 0.0m or 0.0M. The m symbol at the end explicitly indicates that the number is decimal type (by default all real numbers are double type). The numbers closest to 0 that can be stored in decimal are ±1.0 × 10^-28. It is evident that decimal cannot store very large positive and negative numbers (for example with hundreds of digits), nor values very close to 0. On the other hand, this type rarely causes any errors upon financial calculations because it represents the numbers as a sum of the power of the number 10, upon which the round-off errors are much less compared to when we use binary representation. Real numbers of decimal type are exceptionally suitable for performing monetary calculations – calculation of incomes, liabilities, taxes, interest, etc.
|
This way we solved successfully the first sub-problem.
Converting the Input Data into Appropriate Types
The next step is to convert the input data into appropriate types, in order to be able to perform the needed calculations. We select Int32 or int as an appropriate type, because the condition of the problem says that the input data must be within a particular range, for which this data type is completely sufficient. We will do the conversion in the following way:

Helper Variable
We initially store one variable that will be used multiple times. This centralization approach gives us flexibility and possibility to modify the end result of the program with minimum efforts. In case we need to change the value, we must do it in only once place in the code, which saves us time and effort.
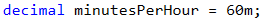
| Avoiding repetitive code (centralization of the program logic) in the tasks that we examine in the present book may look unnecessary at first glance, but this approach is very important upon building large applications in a real work environment, and its exercising in an initial stage of training will help you build a quality programming style. |
Calculating Travel Distance
We calculate the travel time (in hours) by dividing the time by 60 (minutes in an hour). The travel distance is calculated by multiplying the starting speed by the time passed (in hours). After that we change the speed by increasing it by 10%, as per the task description. Calculating the percentage, as well as the following distances passed, is done in the following way:
- The time frame (in hours) is calculated by dividing the provided time frame in minutes by the minutes that are contained in an hour (60).
- The distance passed is calculated by multiplying the time frame (in hours) by the speed that is obtained after the increase.
- The next step is to decrease the speed by 5%, as per the problem description.
- We calculate the remaining distance in the manner described in the first two points.

Calculating and Printing the Output
Up until now we were able to solve two of the most important sub-problems, namely the data input and their processing. What remains is to calculate the end result. As by the description we are required to format it up to 2 symbols after the decimal point, we can do this in the following manner:

If you worked accurately and wrote the program using the input data given in the task description, you will be convinced that it works properly.
Testing in the Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/517#0.