Problem: Numerical Expression

Bonny is an exceptionally powerful witch. As her natural power is not sufficient to successfully fight vampires and werewolves, she has started to master the power of Expressions. An expression is very hard to master, because the spell relies on the ability to quickly solve mathematical expressions.

In order to use an "Expression spell", the witch must know the result of a mathematical expression in advance. An Expression spell consists of a few simple mathematical expressions. Each mathematical expression can contain operators for summing up, subtraction, multiplying and/or division.

The expression is solved without considering the mathematical rules for calculating numerical expressions. This means that the priority is applied according to the sequence of the operators, and not the type of calculation that they do. The expression can contain brackets, as everything inside the brackets is calculated first. Every expression can contain multiple brackets, but no nested brackets:

• An expression containing (…(…)…) is an invalid one.
• An expression containing (…)…(…) is a valid one.

Example

The expression

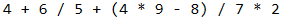
is solved in the following way:

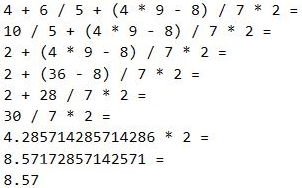
Bonny is very pretty, but not as wise, so she will need our help to master the power of Expressions.

Input Data

The input data consists of a single text line, passed from the console. It contains a mathematical expression for calculation. The line always ends with the "=" symbol. The "=" symbol means end of the mathematical expression.

The input data is always valid and always in the described format. No need to validate it.

Output Data

The output data must be printed on the console. The output consists of one line: the result of the calculated mathematical expression, rounded up to the second digit after the decimal point.

Constraints

• The expressions will consist of maximum 2500 symbols.
• The numbers of each mathematical expression will be within the range [1 … 9].
• The operators in the mathematical expressions will always be among + (summing up), - (subtraction), / (division) or * (multiplying).
• The result of the mathematical expression will be within the range [-100000.00 … 100000.00].
• Allowed execution time: 0.1 seconds.
• Allowed memory: 16 MB.

Sample Input and Output

Hints and Guidelines

As usual, we will first read and process the input, after that we will solve the problem, and finally, we will print the result, formatted as required.

Reading the Input Data

The input data will consist of exactly one text line read from the console. Here we have two ways to process the input. The first way is by reading the entire line using the Console.ReadLine() command and accessing each symbol (char) of the line via a foreach loop. The second one is by reading the input symbol by symbol using the Console.Read() command and processing each symbol.

We will use the second option to solve the problem.

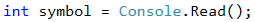
Creating Helper Variables

For the goals of our task we need two variables:

• One variable where we will store the current output.
• One variable where we will store the current operator of our expression.

We will clarify two details regarding the aforementioned code. The first one is the use of decimal type for storing the output of our expression in order to avoid any problems with the accuracy pertaining to the float and double type. The second one is the default value of the operator – it is +, so that the very first number can be added to our output.

Defining the Program Structure

Now that we already have our starting variables, we must decide what will be the main structure of our program. By the requirements we understand that each expression ends with =, i.e. we must read and process symbols until we reach a =. This is followed by an accurately written while loop.

The next step is the processing of our symbol variable. We have 3 possible cases for it:

• If the symbol is a start of a sub-expression placed in brackets i.e. the found symbol is a (.
• If the symbol is a digit between 0 and 9. But how can we check this? How can we check if our symbol is a digit? We can use for assistance the ASCII code of the symbol, via which we can use the following formula: [ASCII code of our symbol] – [ASCII code of the symbol 0] = [the digit that represents the symbol]. If the result of this condition is between 0 and 9, then our symbol is really a number.
• If the symbol is an operator, i.e. it is +, -, * or /.

Implementing the Proposed Idea

Let's examine the actions that we need to undertake in the relevant cases that we defined:

• If our symbol is an operator, then the only thing we need to do is to set a new value for the expressionOperator variable.
• If our symbol is a digit, then we need to change the current result of the expression depending on the current operator, i.e. if expressionOperator is a -, then we must decrease the result by the numerical representation of the current symbol. We can get the numerical representation of the current symbol via the formula that we used upon checking the condition for this case (the [ASCII code of our symbol] – [the ASCII code of the symbol0] = [the digit that represents the symbol])

This is a sample code, implemented the above idea:

• If our symbol is a (, this indicates the beginning of a sub-expression (an expression in brackets). By definition, the sub-expression must be calculated before modifying the result of the whole expression (the actions in brackets are performed first). This means that we will have a local result for the sub-expression and a local operator.

Calculating the Sub-Expression Value

After that, in order to calculate the sub-expression value, we will use the same methods that we used for calculating the main expression – we use a while loop to read symbols (until we reach an ) symbol). Depending on whether the read symbol is a number or an operator, we modify the result of the sub-expression. The implementation of these operations is identical to the above described implementation for calculating expressions. This is why we believe the reader will be able to easily handle it.

After finishing the result calculation for our sub-expression, we modify the result of the whole expression depending on the value of the expressionOperator.

Formatting the Output

The only output that the program must print on the console is the result of solving the expression with accuracy of up to two symbols after the decimal point. How can we format the output this way? We will leave the answer to this question to the reader.

Testing in the Judge System

Test your solution here: https://judge.softuni.org/Contests/Practice/Index/519#1.