Problem: Point on a Segment
The next sample exam problem is about checking whether given point stays inside or outside given horizontal segment.
Video: Point on a Segment
Watch the video lesson about solving the "Point on a Segment" problem: https://youtu.be/isrSHqLvV90.
Problem Description
A horizontal segment is placed on a horizontal line, set with the x coordinates of both ends: first and second. A point is located on the same horizontal line and is set with its x coordinate. Write a program that checks whether the point is inside or outside the segment and calculates the distance to the nearest end of the segment.
Input
The console reads 3 integer numbers (one per line):
- On the first line the number "first" is read – one end of the segment.
- On the second line the number "second" is read – the other end of the segment.
- On the third line the number "point" is read – the location of the point.
All input numbers are integers in the range [-1000 … 1000].
Output
Print the result on the console:
- On the first line, print "in" or "out" – whether the point is inside or outside the segment.
- On the second line, print the distance from the point to the nearest end of the segment.
Sample Input and Output
| Input | Output | Visualization |
|---|---|---|
| 10 5 7 |
in 2 |
 |
| Input | Output | Visualization |
|---|---|---|
| 8 10 5 |
out 3 |
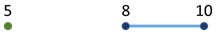 |
| Input | Output | Visualization |
|---|---|---|
| 1 -2 3 |
out 2 |
 |
Reading the Input Data
We read the input from the console.

Calculate the Minimum Distance to the Closest End of the Segment
Since we do not know which point is on the left and which is on the right, we will create two variables to mark this. Since the left point is always the one with the smaller x coordinate, we will use Math.Min(…) to find it. Accordingly, the right one is always the one with a larger x coordinate and we will use Math.Max(…). We will also find the distance from point x to the two points. Because we do not know their position relative to each other, we will use Math.Abs(…) to get a positive result.
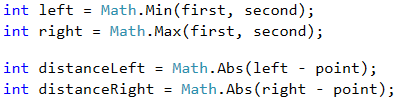
The shorter of the two distances we can found using Math.Min(…).
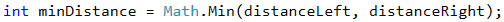
Determining if Point is In or Out the Segment and Printing the Result
What remains is to find whether the point is on or out of the line. The point will be on the line whenever it matches one of the other two points or its x coordinate lies between them. Otherwise, the point is outside the line. After checking, we display one of the two messages, depending on which condition is satisfied.

Finally, we print the distance previously found.

Testing in the Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/516#2.